How Respawn Works

This post is mainly a reminder to myself when inevitably I forget what I was doing when designing Respawn. The general problem space is something I've covered quite a lot, but I haven't really walked through how Respawn works internally.

The general problem is trying to find the correct order of deletion for tables when you have foreign key constraints. You can do something like:

ALTER TABLE [Orders] NOCHECK CONSTRAINT ALL;
ALTER TABLE [OrderLineItems] NOCHECK CONSTRAINT ALL;
DELETE [Orders];
DELETE [OrderLineItems];
ALTER TABLE [Orders] WITH CHECK CHECK CONSTRAINT ALL;
ALTER TABLE [OrderLineItems] WITH CHECK CHECK CONSTRAINT ALL;

You just ignore what order you can delete things in by just disabling all constraints, deleting, then re-enabling. Unfortunately, this results in 3x as many SQL statements over just DELETE, slowing down your entire test run. Respawn fixes this by building the list of DELETE intelligently, and with 3.0, detecting circular relationships. But how?

Traversing a graph

Assuming we've properly set up foreign key constraints, we can view our schema through its relationships:

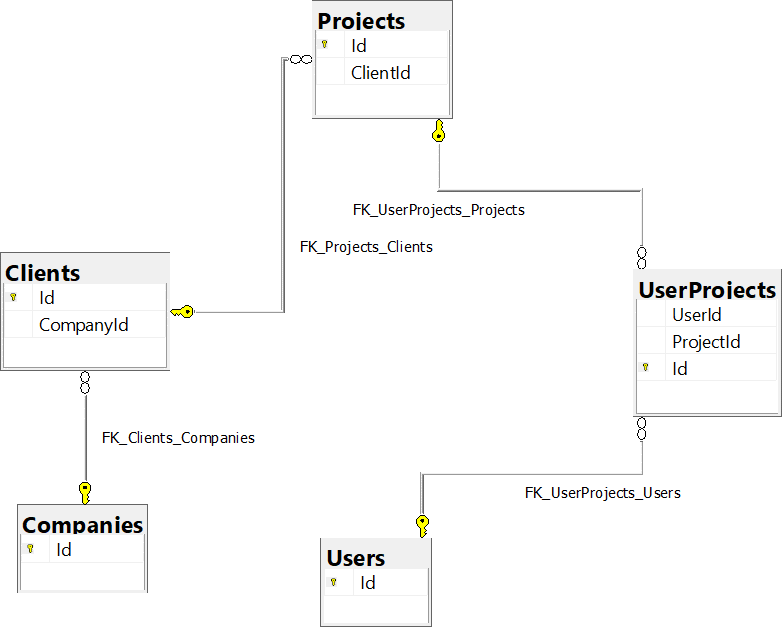
Another way to think about this is to imagine each table as a node, and each foreign key as an edge. But not just any kind of edge, there's a direction. Putting this together, we can construct a directed graph:

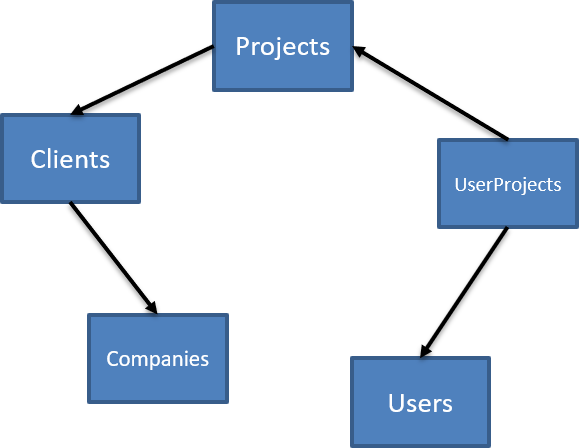
There's a special kind of graph, a directed acyclic graph, where there are no cycles, but we can't make that assumption. We only know there are directed edges.

So why do we need this directed graph? Assuming we don't have any kind of cascades set up for our foreign keys, the order in which we delete tables should start tables with no foreign keys, then tables that reference those, then those that reference those, and so on until we reach the last table. The table that we delete first are those with no foreign keys pointing to it - because no tables depend on it.

In directed graph terms, this is known as a depth-first search. The ordered list of tables is found by conducting a depth-first search, adding the nodes at the deepest first until we reach the root(s) of the graph. When we're done, the list to delete is just the reversed list of nodes. As we traverse, we keep track of the visited nodes, exhausting our not-visited list until it's empty:

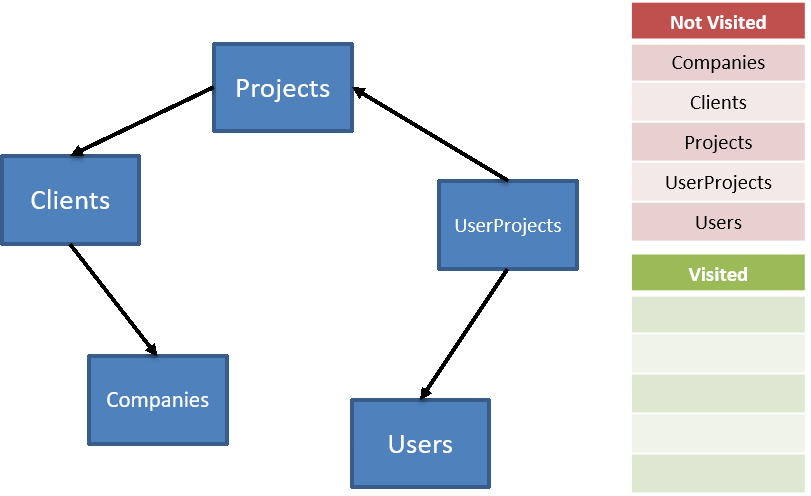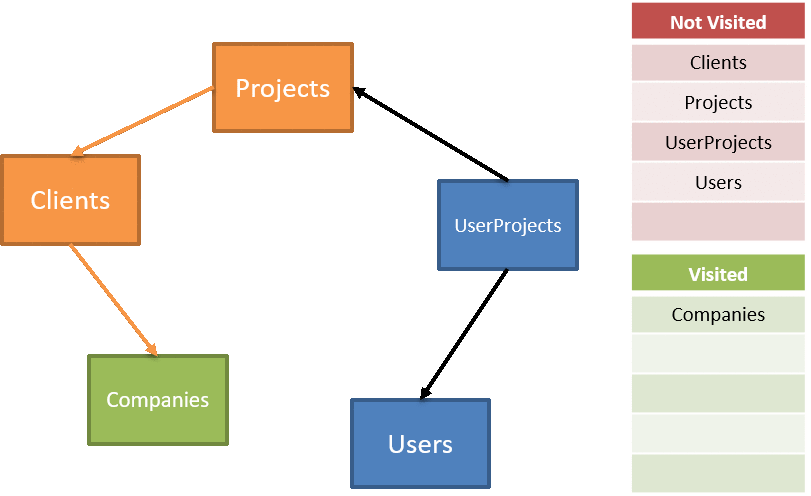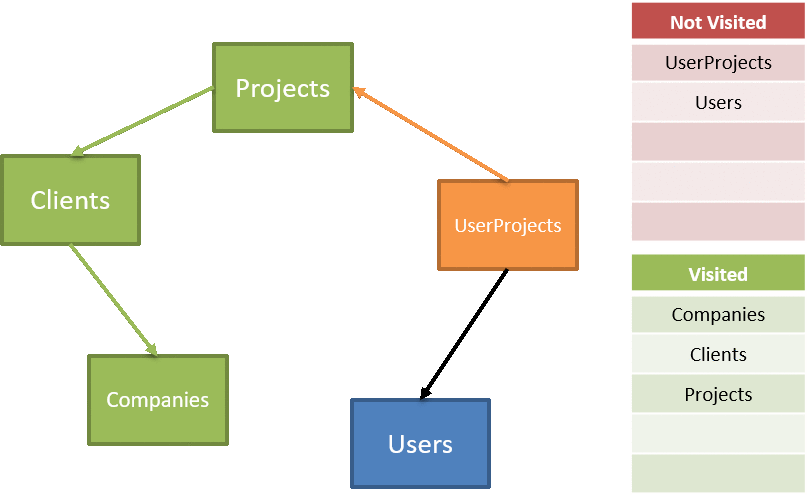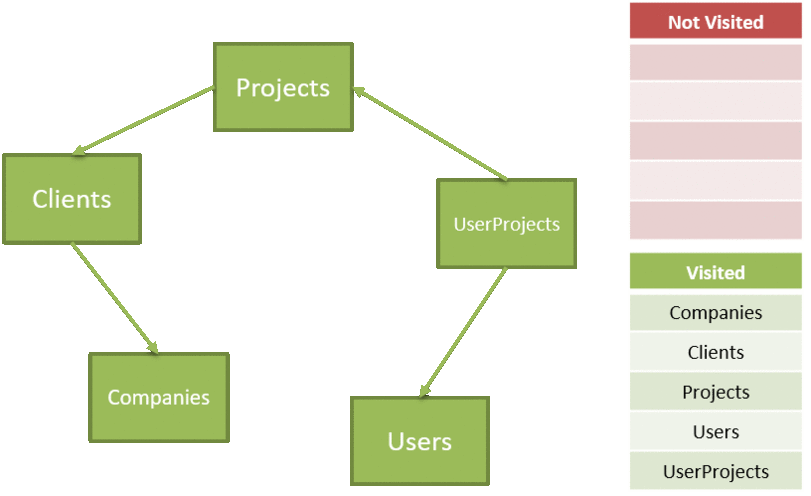
The code for traversing is fairly straightforward, first we need to kick off the traversal based on the overall (unordered) list of tables:

private static List<Table> BuildDeleteList(
    HashSet<Table> tables)
{
    var toDelete = new List<Table>();
    var visited = new HashSet<Table>();

    foreach (var table in tables)
    {
        BuildTableList(table, visited, toDelete);
    }

    return toDelete;
}

Then we conduct our DFS, adding tables to our toDelete list once we've searched all its relationships recursively:

private static void BuildTableList(
    Table table, HashSet<Table> visited, List<Table> toDelete)
{
    if (visited.Contains(table))
        return;

    foreach (var rel in table.Relationships)
    {
        BuildTableList(rel.ReferencedTable, visited, toDelete);
    }

    toDelete.Add(table);
    visited.Add(table);
}

Not pictured - constructing our Table with its Relationships, which is just a matter of querying the schema metadata for each database, and building the graph.

To actually execute the deletes, we just build DELETE statements in the reverse order of our list, and we should have error-free deletions.

This technique works, as we've shown, as long as there are no cycles in our graph. If our tables somehow create a cycle (self-referencing tables don't count, databases can handle a single DELETE on a table with relationships with itself), then our DFS will continue to traverse the cycle infinitely, until we hit a StackOverflowException.

With Respawn 3.0, I wanted to fix this.

Dealing with cycles

There's lots of literature and examples out there on detecting cycles in a directed graph, but I don't just need to detect a cycle. I have to understand, what should I do when I detect a cycle? How should this affect the overall deletion strategy?

For this, it really depends on the database. The overall problem is the foreign key constraints prevent us from deleting with orphans, but with a cycle in our graph, I can't delete tables one-by-one.

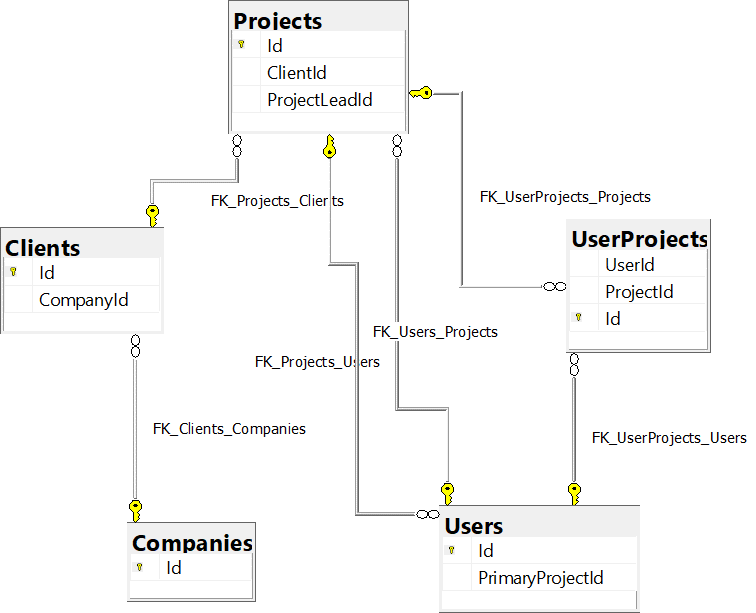
We could try to re-model our schema to remove the cycle, but above, the cycle might make the most sense. A project as a single project lead, and for a user, they have a primary project they work on. Ignoring how we'd figure it out, what would be the right set of commands to do? We still have to worry about the rest of the tables, too.

What we'd like to do is find the problematic tables and just disable the constraints for those tables (or disable those constraints). This depends on the database, however, on how we can disable constraints. Each database is slightly different:

• SQL Server - per constraint or table
• PostgreSQL - per table
• Oracle - per constraint
• MySQL - entire session

For MySQL, this makes our job a bit easier. We can disable constraints at the beginning of our deletion, and the order of the tables no longer matters.

The other databases can disable individual constraints and/or constraints for the entire table. Given the choice, it's likely fewer SQL statements just to disable for tables, but Oracle lets us only disable individual constraints. So that means that our algorithm must:

• Find ALL cycles (not just IF there is a cycle)
• Find all tables and relationships involved the cycles
• Identify these problematic relationships when traversing

Our updated graph now looks like:

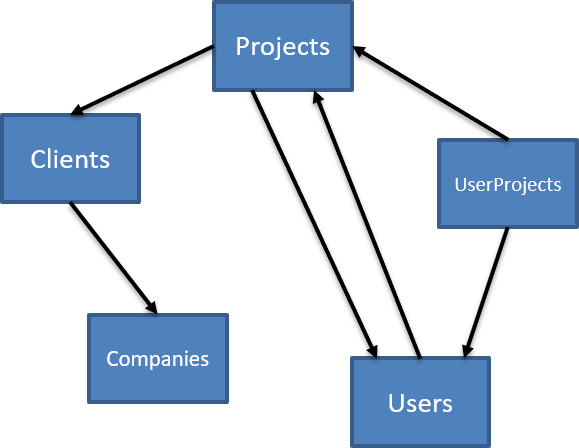
We need to detect the relationship between Projects and Users, keep those in a list, and finally note those relationships when traversing the entire graph.

In order to find all the cycles, once we find one, we can note it, continuing on instead of repeating the same paths:

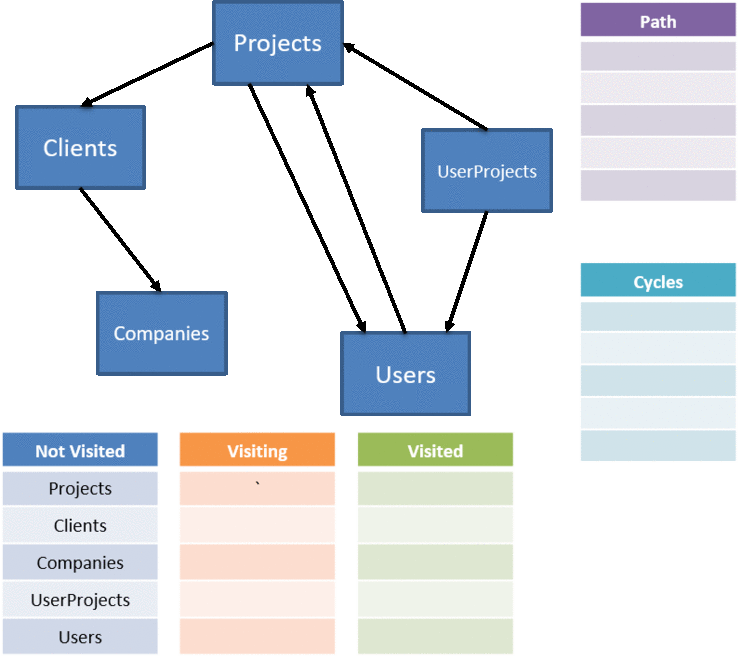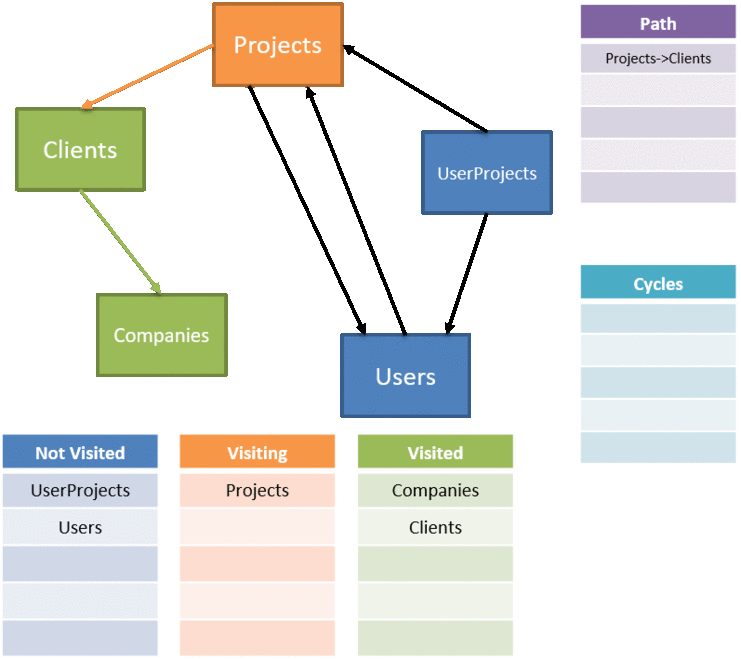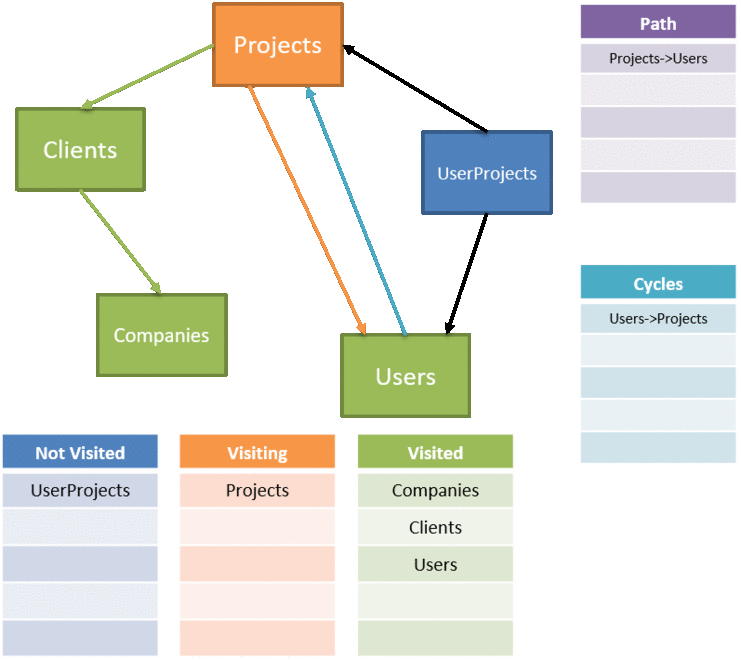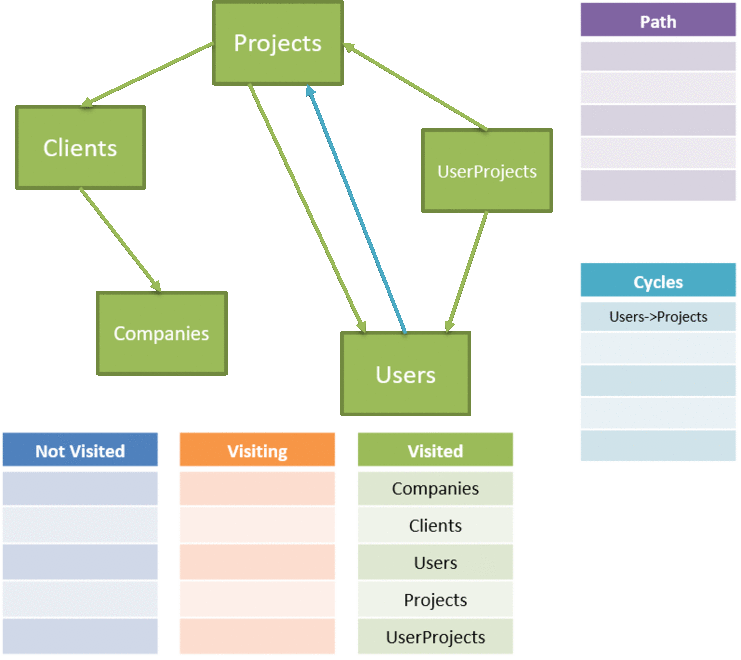
We need to alter our algorithm a bit, first to keep track of our new lists for not visited, visiting, and visited. We also need to return not just the ordered list of tables to delete via a stack, but the set of relationships that we identified as causing a cycle:

private static bool HasCycles(Table table,
    HashSet<Table> notVisited,
    HashSet<Table> visiting,
    HashSet<Table> visited,
    Stack<Table> toDelete,
    HashSet<Relationship> cyclicalRelationships
    )
{
    if (visited.Contains(table))
        return false;

    if (visiting.Contains(table))
        return true;

    notVisited.Remove(table);
    visiting.Add(table);

    foreach (var relationship in table.Relationships)
    {
        if (HasCycles(relationship.ReferencedTable, 
            notVisited, visiting, visited, toDelete, cyclicalRelationships))
        {
            cyclicalRelationships.Add(relationship);
        }
    }

    visiting.Remove(table);
    visited.Add(table);
    toDelete.Push(table);

    return false;
}

Walking through the code, we're examining one table at a time. If the set of visited tables already contains this table, there's nothing to do and we can just return false.

If, however, the set of currently visiting tables contains the table then we've detected a cycle, so return true.

Next, we move our table from the set of notVisited to currently visiting tables. We loop through our relationships, to see if any complete a cycle. If that relationship does, we add that relationship to the set of cyclical relationships.

Finally, once we're done navigating our relationships, we move our table from the set of visiting to visited tables, and push our table to the stack of tables to delete. We switched to a stack so that we can just pop off the tables and that becomes the right order to delete.

To kick things off, we just loop through the collection of all our tables, checking each for a cycle and building up our list of tables to delete and bad relationships:

private static (HashSet<Relationship> cyclicRelationships, Stack<Table> toDelete) 
    FindAndRemoveCycles(HashSet<Table> allTables)
{
    var notVisited = new HashSet<Table>(allTables);
    var visiting = new HashSet<Table>();
    var visited = new HashSet<Table>();
    var cyclicRelationships = new HashSet<Relationship>();
    var toDelete = new Stack<Table>();

    foreach (var table in allTables)
    {
        HasCycles(table, notVisited, visiting, visited, toDelete, cyclicRelationships);
    }

    return (cyclicRelationships, toDelete);
}

It's expected that we'll visit some tables twice, but that's a quick check in our set and we only traverse the entire graph once.

Now that we have our list of bad tables/relationships, we can apply the right SQL DDL to disable/enable constraints intelligently. By only targeting the bad relationships, we can minimize the extra DDL statements by adding just add a single DDL statement for each cycle found.